高度场
1、总体介绍
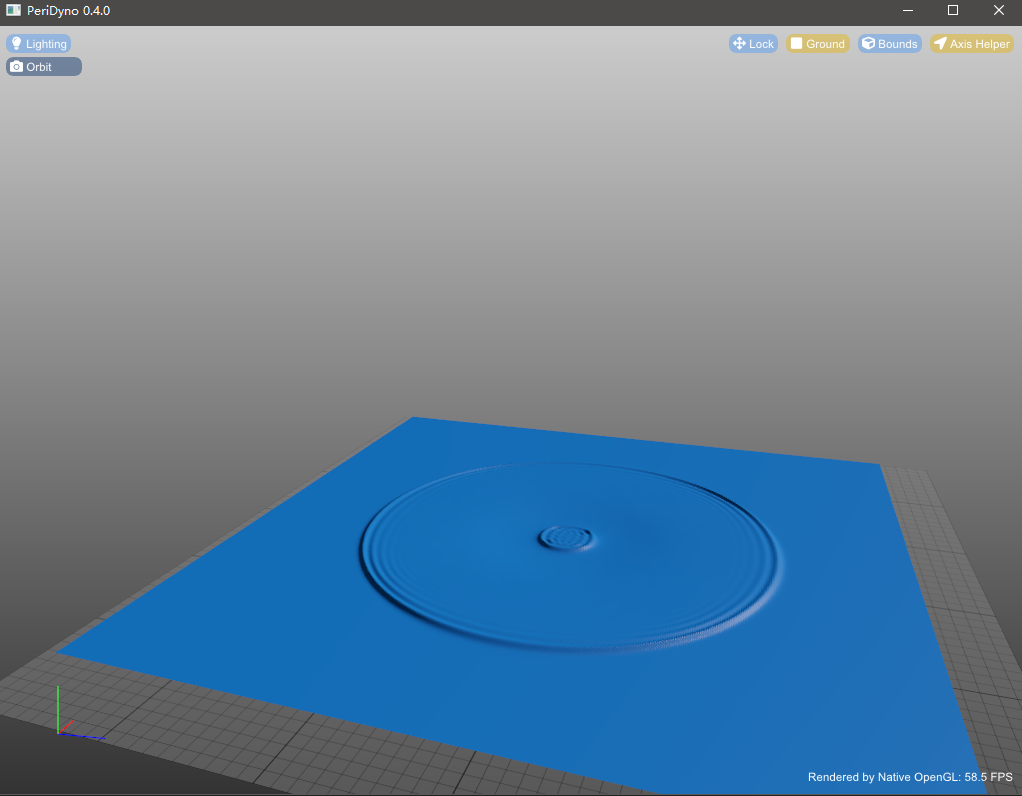
高度场流体仿真分为两个部分,基于浅水方程(SWE)的浅水波模拟和基于快速傅里叶变换(FFT)的海浪模拟。浅水方程(SWE)是描述浅水流动的数学模型,同时也是水力学中的一个重要的数学模型。浅水方程建立在具有物理意义的物理量守恒基础上,也可以称为双曲守恒型方程组。基于快速傅里叶变换(FFT)的海浪模拟的主要思想就是按照Phillips波普得到海面的高度场(也就是傅里叶变换的频域),然后将其逆傅里叶变换(IFFT)得到海面(也就是时域)。
2、浅水波仿真
目前实时系统大规模水体仿真广泛使用Gerstner模型,其核心思想是通过对计算格点的位置进行周期性的偏移来达到水波翻滚的效果。尽管Gerstner Wave适用于建模大范围的水体,然而其在展现精细尺度水波上能力有限,且无法反应水体与刚体的交互。鉴于此,本项目使用浅水方程来实现精细尺度的水波模拟:
\begin{array}{l}
\frac{{\partial h}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {hu} \right) + \frac{\partial }{{\partial y}}\left( {hv} \right) = 0 \\
\frac{\partial }{{\partial t}}\left( {hu} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{h{u^2}}}{2}} \right) + \frac{\partial }{{\partial y}}\left( {huv} \right) = - gh\frac{{\partial s}}{{\partial x}} \\
\frac{\partial }{{\partial t}}\left( {hv} \right) + \frac{\partial }{{\partial x}}\left( {huv} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{h{v^2}}}{2}} \right) = - gh\frac{{\partial s}}{{\partial y}}
\end{array}
其中u、v分别表示洋流水平速度的两个分量,h表示洋流的深度,s表示海面垂直坐标,g表示重力加速度。求解过程,首先基于高度场对仿真区域进行如图所示的离散。
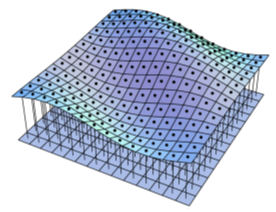
然后,通过求解波动方程计算每个时刻的高度场的位置。最终,将基于浅水方程(SWE)得到的高度场叠加到大区域水体上从而实现更加逼得水体仿真。
首先初始化水面的初始高度。对于水面边界的高度进行处理,每次计算后:
a) x=0点的粒子高度值等于x=1点的粒子高度值;
b) x= width - 1点的粒子高度值等于x= width - 2点的粒子高度值;
c) y=0点的粒子高度值等于y=1点的粒子高度值;
d) y= height- 1点的粒子高度值等于y= height - 2点的粒子高度值。
src/Dynamics/HeightField/CapillaryWave.cu 中实现如下:
__global__ void C_ImposeBC(Vec4f* grid_next, Vec4f* grid, int width, int height, int pitch)
{
int x = threadIdx.x + blockIdx.x * blockDim.x;
int y = threadIdx.y + blockIdx.y * blockDim.y;
if (x < width && y < height)
{
if (x == 0)
{
Vec4f a = grid[(y)*pitch + 1];
grid_next[(y)*pitch + x] = a;
}
else if (x == width - 1)
{
Vec4f a = grid[(y)*pitch + width - 2];
grid_next[(y)*pitch + x] = a;
}
else if (y == 0)
{
Vec4f a = grid[(1) * pitch + x];
grid_next[(y)*pitch + x] = a;
}
else if (y == height - 1)
{
Vec4f a = grid[(height - 2) * pitch + x];
grid_next[(y)*pitch + x] = a;
}
else
{
Vec4f a = grid[(y)*pitch + x];
grid_next[(y)*pitch + x] = a;
}
}
}
对每个时间内的高度场进行迭代:
__global__ void C_OneWaveStep(Vec4f* grid_next, Vec4f* grid, int width,
int height, float timestep, int pitch)
最后计算u、v洋流水平速度的两个分量,h洋流的深度,s海面垂直坐标。
__global__ void C_InitHeightField(
Vec4f* height,
Vec4f* grid,
int patchSize,
float horizon,
float realSize)
{
int i = threadIdx.x + blockIdx.x * blockDim.x;
int j = threadIdx.y + blockIdx.y * blockDim.y;
if (i < patchSize && j < patchSize)
{
int gridx = i + 1;
int gridy = j + 1;
Vec4f gp = grid[gridx + patchSize * gridy];
height[i + j * patchSize].x = gp.x - horizon;
float d = sqrtf((i - patchSize / 2) * (i - patchSize / 2) + (j - patchSize / 2) * (j - patchSize / 2));
float q = d / (0.49f * patchSize);
float weight = q < 1.0f ? 1.0f - q * q : 0.0f;
height[i + j * patchSize].y = 1.3f * realSize * sinf(3.0f * weight * height[i + j * patchSize].x * 0.5f * M_PI);
}
}
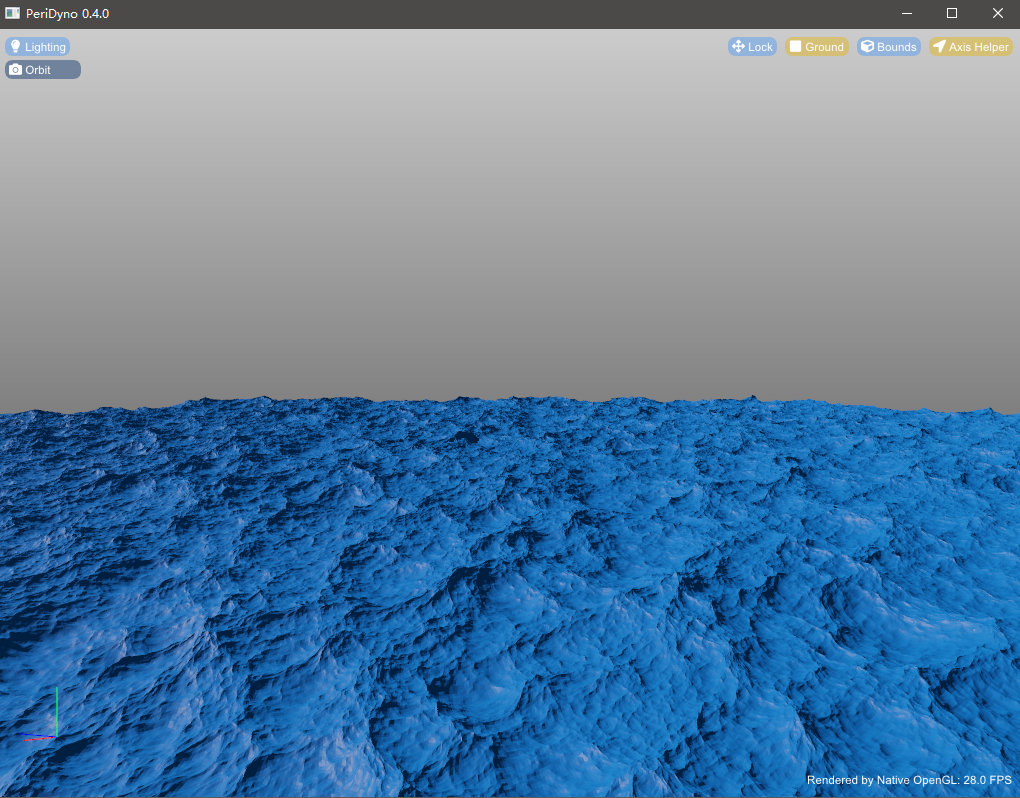
3、基于快速傅里叶变换(FFT)的海浪模拟
FFT模型是一种统计模型。不同于Gerstner模型采用多个正弦余弦函数去拟合,FFT模型采用傅里叶变换的方式。傅里叶变换的核心就是用sin(nx)和cos(nx)去模拟任意的周期函数。在FFT模型中,用时间和水平高度的随机函数h(x,t)来表示浪的高度。该方法仿真度高,易于建模,其计算公式如下[1]:
$$h(X,t) = \sum\limits_K^{} {\tilde h(K,t){{\mathop{\rm e}\nolimits} ^{(iK{\rm{X}})}}} $$
式中,$X{\rm{ = }}(x,z)$水平位置;$t$代表时间;$K$是一个二维向量;$\tilde h(k,t)$表示海浪表面结构。
构建FFT模型的高度场之后,接下来创建随机的高度场。引入高斯随机函数,有:
$${\tilde h_0}(K) = \frac{1}{{\sqrt 2 }}({\xi _r} + i{\xi _i})\sqrt {{P_h}(K)} $$
其中,${\xi _r}$和${\xi _i}$是相互独立的高斯随机数(均值为 0,方差为 1)。此时在$t$时刻波的振幅为:
$$\tilde h(K,t) = \tilde h(K){e^{i\omega (K)t}} + \tilde h_0^*( - K){e^{ - i\omega ({\rm{K}})t}}$$ 其中,$\omega (k)$是波$K$的角频率,可以根据${\omega ^2}(k) = g|K|$计算得到;*号表示复数的共轭运算。根据FFT模型,海浪的高度最终一定为实数,所以一定满足$\tilde h(-K)= \tilde h_0^*(K)$。
template<typename TDataType>
void OceanPatch<TDataType>::generateH0(Vec2f* h0)
{
for (unsigned int y = 0; y <= mResolution; y++)
{
for (unsigned int x = 0; x <= mResolution; x++)
{
float kx = (-( int )mResolution / 2.0f + x) * (2.0f * CUDART_PI_F / m_realPatchSize);
float ky = (-( int )mResolution / 2.0f + y) * (2.0f * CUDART_PI_F / m_realPatchSize);
float P = sqrtf(phillips(kx, ky, windDir, m_windSpeed, A, dirDepend));
if (kx == 0.0f && ky == 0.0f)
{
P = 0.0f;
}
float Er = gauss();
float Ei = gauss();
float h0_re = Er * P * CUDART_SQRT_HALF_F;
float h0_im = Ei * P * CUDART_SQRT_HALF_F;
int i = y * mSpectrumWidth + x;
h0[i].x = h0_re;
h0[i].y = h0_im;
}
}
}
初始化相位和振幅。频谱可以采用Phillips频谱。Phillips频谱适用于海面网格并行化计算。它是一种真实度较高的频谱,多用于在有风的影响下。Phillips频谱的定义如下:
$${P_h}(K) = A\frac{{\exp ( - 1/{{(kL)}^2})}}{{{k^4}}}|\hat K\hat \omega {|^2}$$
其中,$g$表示重力加速度;$k = |K| = 2\pi / \lambda $;$\lambda $表示波长;$A$表示一个常系数;$L = {V^2}/g$表示风速在$V$的情况下产生的最大波浪;$\hat \omega $表示风向;$|\hat K\hat \omega {|^2}$表示消除了垂直于风向运动的波。
// generate wave heightfield at time t based on initial heightfield and dispersion relationship
__global__ void generateSpectrumKernel(Vec2f* h0,
Vec2f* ht,
unsigned int in_width,
unsigned int out_width,
unsigned int out_height,
float t,
float patchSize)
{
unsigned int x = blockIdx.x * blockDim.x + threadIdx.x;
unsigned int y = blockIdx.y * blockDim.y + threadIdx.y;
unsigned int in_index = y * in_width + x;
unsigned int in_mindex = (out_height - y) * in_width + (out_width - x); // mirrored
unsigned int out_index = y * out_width + x;
// calculate wave vector
Vec2f k;
k.x = (-( int )out_width / 2.0f + x) * (2.0f * CUDART_PI_F / patchSize);
k.y = (-( int )out_width / 2.0f + y) * (2.0f * CUDART_PI_F / patchSize);
// calculate dispersion w(k)
float k_len = sqrtf(k.x * k.x + k.y * k.y);
float w = sqrtf(9.81f * k_len);
if ((x < out_width) && (y < out_height))
{
Vec2f h0_k = h0[in_index];
Vec2f h0_mk = h0[in_mindex];
// output frequency-space complex values
ht[out_index] = complex_add(complex_mult(h0_k, complex_exp(w * t)), complex_mult(conjugate(h0_mk), complex_exp(-w * t)));
//ht[out_index] = h0_k;
}
}
在使用FFT模型在流体仿真的过程中,需要根据每个点的斜率之计算表面的法向量。在实际的计算过程中,一般采用邻近网格点有限差分来计算斜率值。但为了减少小波波长的斜率误差,可使用反向FFT变换的方式进行求解:
$$\nabla h(X,t) = \sum\limits_K^{} {iK\tilde h(K,t)\exp (iKX)} $$
cufftExecC2C(fftPlan, (float2*)m_ht, (float2*)m_ht, CUFFT_INVERSE);
cufftExecC2C(fftPlan, (float2*)m_Dxt, (float2*)m_Dxt, CUFFT_INVERSE);
cufftExecC2C(fftPlan, (float2*)m_Dzt, (float2*)m_Dzt, CUFFT_INVERSE);
此外,还需要一个偏置向量D(x,t)来模拟海水的浪尖,可以如下设置:
$$D(x,t) = \sum\limits_k { - i\frac{k}{{|k|}}h(k,t){e^{ikx}}} $$
其中雅克比矩阵为:
\begin{equation}
J\left( x \right) =\left| \begin{matrix}
J_{xx}& J_{xy}\\
J_{zx}& J_{yy}\\
\end{matrix} \right|
\end{equation}
$$
\begin{array}{l}
J_{xx}=\frac{\partial x^{'}}{\partial x}=1+\lambda \frac{\partial D_x\left( x,t \right)}{\partial x}\\
J_{yy}=\frac{\partial y^{'}}{\partial y}=1+\lambda \frac{\partial D_y\left( x,t \right)}{\partial y}\\
J_{yx}=\frac{\partial y^{'}}{\partial x}=\lambda \frac{\partial D_y\left( x,t \right)}{\partial x}\\
J_{xy}=\frac{\partial x^{'}}{\partial y}=\lambda \frac{\partial D_x\left( x,t \right)}{\partial y}\\
\end{array}
$$
参考文献
[1] Tessendorf J. Simulating ocean water[J]. Simulating nature: realistic and interactive techniques. SIGGRAPH, 2001, 1(2): 5.