粒子系统
PeriDyno中的粒子系统主要用于模拟流体材料。该系统中,流体材料会被离散为粒子。通过计算每个粒子在Navior Stokes 方程作用下的运动,即可实现流体的模拟。现阶段PeriDyno的粒子系统中包含有以下几部分模块:基于SPH的投影法求解器、人工粘性求解器和表面张力求解器,以及PBF(Position Based Fluid)求解器等。以下是粒子系统相关基础理论以及求解器的介绍。
1. 基础理论
流体的Navior Stokes方程的具体形式如下:
$$ \begin{aligned} &\rho\frac{\mathrm{D} \mathbf{v} }{\mathrm{D} t} = - \nabla p + \nabla\cdot \mu (\nabla\mathbf{V}+\nabla\mathbf{V}^T)+\mathbf{F} \end{aligned} $$ (公式1)
其中,$\rho$、$\mathbf{v}$、$p$、$\mu$、$\mathbf{f}$ 分别为流体的密度场、速度场、压强场、粘性系数以及流体所受到的体积力。该方程的本质为的动量守恒定律,其等式右端各项的物理含义分别为流体不可压缩性引起的压强作用、流体的粘性引起的剪切力作用,以及流体所受到的重力、离心力等体积力的作用。
除NS方程外,大多数流体在运动过程中还需要满足不可压缩性性条件,即:
$$ \nabla \cdot \mathbf{V} = \frac{1}{\rho}\frac{\mathrm{d} \rho}{\mathrm{d} t} = 0 $$
(公式2)
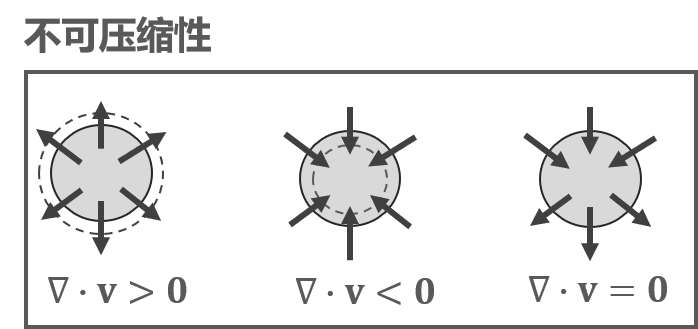
当流体某位置的不可压缩性条件存在被破坏的趋势时,相应位置上会产生一定的压强以抵抗不可压缩性的破坏。
2. 流体模拟的基本方法
虽然理论上联立Navior Stokes 方程(公式一)和不可压缩性条件(公式二)求解出流体的速度场,即可实现流体运动的模拟。然而直接求解这两个方程是很困难的。为了简化上述量微分方程求解的难度,我们需要采用以下两种技术手段:
-
粒子离散化。使用携带有质量、压强等物理信息的粒子离散流体连续的物理场和微分算子,进而将上述连续形式的微分方程转化为线性方程组。

-
算子分裂法。将Navior Stokes方程拆分成三个较小的微分方程,以简化原微分方程求解的难度。
在使用粒子离散化与算子分裂法后,原Navior Stokes方程就被转化为如下三组方程组:
-
只有体积力项的速度微分方程。 流体粒子在体积力作用下速度的变化。 $$ \frac{\mathbf{v}_i^{n+\frac{1}{3}} - \mathbf{v}_i^{old} }{\delta t} = \mathbf{F}
$$ -
只有粘性项的微分方程(流体的粘性)。 不可压缩性作用下的流体速度场变化。 $$ \frac{\mathbf{v}_i^{n+\frac{2}{3}} - \mathbf{v}_i^{n+\frac{1}{3} }}{\delta t} = \nabla_i\cdot \mu (\nabla\mathbf{V}+\nabla\mathbf{V}^T) $$
-
只有压强项的微分方程(不可压缩性)。 不可压缩性作用下的流体速度场变化。 $$ \frac{\mathbf{v}_i^{new} - \mathbf{v}_i^{n+\frac{2}{3}} }{\delta t} = - \frac{1}{\rho_i} \nabla_i p $$
上式中的$\delta t$为仿真时间步长,$i$为某粒子的编号。其中压强场可以通过流体速度散度误差$\nabla_i\cdot\mathbf{v}$或密度误差$\rho_i-\rho_0$来获得($\rho_0$为流体的静止密度)。
该系统中包含有以下几种基础方法,即:SPH(Smoothed Particle Hydrodynamics)、PBF(Position Based Fluid)法、投影法(Projection Method)等。
3. SPH(Smoothed Particle Hydrodynamics)离散化方法简介
SPH法是最常被使用的一类粒子法。该方法中任意位置 $\mathbf{x}$ 的物理量都可以通过其邻域粒子(邻近粒子)$j$ 插值计算得到,即: $$ A(\mathbf{x})={\sum_{j,\left |\mathbf{x} -\mathbf{x}_j \right | <h}A_j *W(\left |\mathbf{x} -\mathbf{x}_j \right |,h)} $$ (公式3) 其中$h$为平滑半径(SPH支持域半径),$j$为与点$\mathbf{x}$距离小于$h$的粒子编号,$W(r,h)$为高斯函数或具有类似特性样条函数。如果相对于$h$的粒子间距足够小,则由上述方程重建的物理场$A(\mathbf{x})$是较为平滑的。
基于公式3可以实现密度等物理场以及微分算子的离散化。略去推导过程几种常用的微分算子离散化形式为:
4. 粒子系统的核心求解器
基于算子分裂策略,原Navior Stokes方程的求解过程被划分为了三个独立的求解步骤,其中最重要的求解步骤是不可压缩性求解。不可压缩性是指流体运动中始终保持密度不变的特性,该特性直接地影响了流体的运动。目前PeriDyno中不可压缩性的实现方法有两种,分别为“基于位置约束的方法”和“投影法”。这两部分的算法介绍见4.2.2节和4.2.3节。
除不可压缩性计算之外,粘性求解也是流体模拟的重要步骤。PeriDyno中包含有基于非物理的人工粘性求解器,该求解器可以显著提高低流体的稳定性,也能够模拟大粘性流体运动。这部分的介绍见4.2.3节。
此外,为了更准确地模拟小尺度的不可压缩流体运动,也要考虑流体的表面张力作用。这一部分的介绍请参考4.2.4节。

参引文献
[1] Bridson R. Fluid simulation for computer graphics[M]. AK Peters/CRC Press, 2015. [2] Koschier D, Bender J, Solenthaler B, et al. Smoothed particle hydrodynamics techniques for the physics based simulation of fluids and solids[J]. arXiv preprint arXiv:2009.06944, 2020. [3] Monaghan J J. Smoothed particle hydrodynamics[J]. Annual review of astronomy and astrophysics, 1992, 30: 543-574.