刚体动力学
刚体是在运动过程中,形状和大小不变,而且内部各点的相对位置不发生改变的物体。绝对刚体实际上是不存在的,只是一种理想模型,因为任何物体在受力作用后,都或多或少会产生变形。如果变形的程度相对于物体本身几何尺寸来说极为微小,在研究物体运动时变形就可以忽略不计。
1、刚体的三种类型
系统中刚体一共有三种类别,分别是:
(1)动态刚体(dynamic)
- 正质量
- 每帧都更新自己的位置
(2)Kinematic刚体
- 零个质量 -由用户设置
(3)静态的刚体(static)
- 零质量
- 不能移动,但能发生碰撞
2、刚体仿真计算过程
刚体仿真计算过程主要可分为以下几个步骤:
(1)加载模型和场景
(2)根据用户的需求添加约束和碰撞
(3)计算刚体的加速度
(4)更新刚体的速度和位置信息
(5)重复迭代(3)和(4),直到程序结束
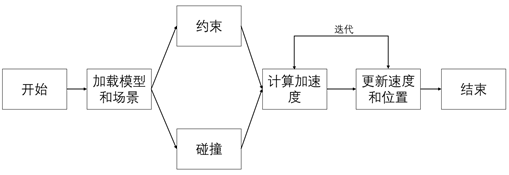
接下来对刚体程序的计算过程进行解释(具体代码参考RigidBody/RigidBodySystem.cu和RigidBody/IterativeConstraintSolver.cu): 在刚体动力学计算过程中,首先处理刚体的碰撞和约束: enforceConstraints()//约束 handleCollision()//碰撞
在处理完刚体约束和碰撞之后,我们先将刚体与地面碰撞的点对信息和刚体与刚体间碰撞的点对信息累加起来。所有的碰撞点对信息记录在allContacts变量中,将碰撞点的总数信息保存到Contacts变量中。
接下来判断刚体是否设置了摩擦力约束。如果没有设置摩擦力约束,刚体是非穿透类型,则只有法线1个约束。如果设置了摩擦力,那么刚体的切平面还有两个约束。因此碰撞点对需要额外开辟2倍法线的空间,即约束的数量是碰撞点对的3倍。
template <typename ContactPair>
__global__ void SetupFrictionConstraints(
DArray<ContactPair> nbq,
int contact_size)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= contact_size) return;
Coord3D n = nbq[pId].normal1;
n /= n.norm();
Coord3D n1, n2;
if (abs(n[1]) > EPSILON || abs(n[2]) > EPSILON)
{
n1 = Coord3D(0, n[2], -n[1]);
n1 /= n1.norm();
n2 = n1.cross(n);
n2 /= n2.norm();
}
else if (abs(n[0]) > EPSILON)
{
n1 = Coord3D(n[2], 0, -n[0]);
n1 /= n1.norm();
n2 = n1.cross(n);
n2 /= n2.norm();
}
nbq[pId * 2 + contact_size].bodyId1 = nbq[pId].bodyId1;
nbq[pId * 2 + contact_size].bodyId2 = nbq[pId].bodyId2;
nbq[pId * 2 + contact_size] = nbq[pId];
nbq[pId * 2 + contact_size].contactType = ContactType::CT_FRICTION;
nbq[pId * 2 + contact_size].normal1 = n1;
nbq[pId * 2 + 1 + contact_size].bodyId1 = nbq[pId].bodyId1;
nbq[pId * 2 + 1 + contact_size].bodyId2 = nbq[pId].bodyId2;
nbq[pId * 2 + 1 + contact_size] = nbq[pId];
nbq[pId * 2 + 1 + contact_size].contactType = ContactType::CT_FRICTION;
nbq[pId * 2 + 1 + contact_size].normal1 = n2;
}
将所有碰撞点对的信息保存到Contacts变量中。
接下来开始进行刚体动力学计算。在解释代码之前,先补充说明整个动力学计算的过程。假设速度从${{\rm{V}}^1}$变化到${{\rm{V}}^2}$的时间步长为$\Delta t $,则此时的加速度可表示为 : $$ \dot{V}\approx \frac{V^2-V^1}{\bigtriangleup t} $$
根据牛顿第二定律可得到: $$ m\dot V = {F_c} + {F_{ext}} $$
其中${F_c}$表示约束力、${F_{ext}}$表示额外力。约束力可表示为${F_c} = {J^T}\lambda$。根据上述两式有: $$ M({V^2} - {V^1}) = \Delta t({J^T}\lambda + {F_{ext}}) $$
因此需要求解$[\lambda ]$进而求出$[{V^2}]$。将问题转换为求解$[\lambda ]$的线性方程$J{\rm{B}}\lambda {\rm{ = }}\eta $。同时根据$B{\rm{ = }}{{\rm{M}}^{ - 1}}{J^T}$,则有:
$$ \eta = \frac{1}{{\Delta t}}\xi - J(\frac{1}{{\Delta t}}{V^1} + {M^{ - 1}}{F_{ext}}) $$
如果约束是一致的,我们可以求解出$\lambda $,进而计算出${V^2}$,从而可以推导出刚体的速度和位移:
\begin{array}{l}
{x^{\rm{2}}}{\rm{ = }}{x^1} + \Delta t{v^2}\\
{q^2} = {q^1} = \frac{{\Delta t}}{2}{q^1}{w^2}
\end{array}
接下来开始对程序进行解释,首先计算雅可比矩阵(Jacobian)J,以及B矩阵。
template <typename Coord, typename Matrix, typename ContactPair>
__global__ void CalculateJacobians(
DArray<Coord> J,
DArray<Coord> B,
DArray<Coord> pos,
DArray<Matrix> inertia,
DArray<Real> mass,
DArray<ContactPair> nbc)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= J.size() / 4) return;
int idx1 = nbc[pId].bodyId1;
int idx2 = nbc[pId].bodyId2;
//printf("%d %d\n", idx1, idx2);
if (nbc[pId].contactType == ContactType::CT_NONPENETRATION) // contact, collision
{
Coord p1 = nbc[pId].pos1;
Coord p2 = nbc[pId].pos2;
Coord n = nbc[pId].normal1;
Coord r1 = p1 - pos[idx1];
Coord r2 = p2 - pos[idx2];
J[4 * pId] = n;
J[4 * pId + 1] = (r1.cross(n));
J[4 * pId + 2] = -n;
J[4 * pId + 3] = -(r2.cross(n));
B[4 * pId] = n / mass[idx1];
B[4 * pId + 1] = inertia[idx1].inverse() * (r1.cross(n));
B[4 * pId + 2] = -n / mass[idx2];
B[4 * pId + 3] = inertia[idx2].inverse() * (-r2.cross(n));
}
else if (nbc[pId].contactType == ContactType::CT_BOUDNARY) // boundary
{
Coord p1 = nbc[pId].pos1;
// printf("@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ %d %.3lf %.3lf %.3lf\n", idx1, p1[0], p1[1], p1[2]);
Coord n = nbc[pId].normal1;
Coord r1 = p1 - pos[idx1];
J[4 * pId] = n;
J[4 * pId + 1] = (r1.cross(n));
J[4 * pId + 2] = Coord(0);
J[4 * pId + 3] = Coord(0);
B[4 * pId] = n / mass[idx1];
B[4 * pId + 1] = inertia[idx1].inverse() * (r1.cross(n));
B[4 * pId + 2] = Coord(0);
B[4 * pId + 3] = Coord(0);
}
else if (nbc[pId].contactType == ContactType::CT_FRICTION) // friction
{
Coord p1 = nbc[pId].pos1;
//printf("~~~~~~~ %.3lf %.3lf %.3lf\n", p1[0], p1[1], p1[2]);
Coord p2 = Coord(0);
if (idx2 != -1)
p2 = nbc[pId].pos2;
Coord n = nbc[pId].normal1;
Coord r1 = p1 - pos[idx1];
Coord r2 = Coord(0);
if (idx2 != -1)
r2 = p2 - pos[idx2];
J[4 * pId] = n;
J[4 * pId + 1] = (r1.cross(n));
if (idx2 != -1)
{
J[4 * pId + 2] = -n;
J[4 * pId + 3] = -(r2.cross(n));
}
else
{
J[4 * pId + 2] = Coord(0);
J[4 * pId + 3] = Coord(0);
}
B[4 * pId] = n / mass[idx1];
B[4 * pId + 1] = inertia[idx1].inverse() * (r1.cross(n));
if (idx2 != -1)
{
B[4 * pId + 2] = -n / mass[idx2];
B[4 * pId + 3] = inertia[idx2].inverse() * (-r2.cross(n));
}
else
{
B[4 * pId + 2] = Coord(0);
B[4 * pId + 3] = Coord(0);
}
}
}
其中B矩阵为$B=M^{-1}J^T$。 接下来计算D矩阵,D=JB。
template <typename Coord>
__global__ void CalculateDiagonals(
DArray<Real> D,
DArray<Coord> J,
DArray<Coord> B)
{
int tId = threadIdx.x + (blockIdx.x * blockDim.x);
if (tId >= J.size() / 4) return;
Real d = Real(0);
d += J[4 * tId].dot(B[4 * tId]);
d += J[4 * tId + 1].dot(B[4 * tId + 1]);
d += J[4 * tId + 2].dot(B[4 * tId + 2]);
d += J[4 * tId + 3].dot(B[4 * tId + 3]);
D[tId] = d;
}
接下来计算$\eta $矩阵$\eta = \frac{1}{{\Delta t}}\xi - J(\frac{1}{{\Delta t}}{V^1} + {M^{ - 1}}{F_{ext}})$:
template <typename Coord, typename ContactPair>
__global__ void CalculateEta(
DArray<Real> eta,
DArray<Coord> velocity,
DArray<Coord> angular_velocity,
DArray<Coord> J,
DArray<Real> mass,
DArray<ContactPair> nbq,
Real dt)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= J.size() / 4) return;
int idx1 = nbq[pId].bodyId1;
int idx2 = nbq[pId].bodyId2;
//printf("from ita %d\n", pId);
Real ita_i = Real(0);
if (true) // test dist constraint
{
ita_i -= J[4 * pId].dot(velocity[idx1]);
ita_i -= J[4 * pId + 1].dot(angular_velocity[idx1]);
if (idx2 != -1)
{
ita_i -= J[4 * pId + 2].dot(velocity[idx2]);
ita_i -= J[4 * pId + 3].dot(angular_velocity[idx2]);
}
}
eta[pId] = ita_i / dt;
if (nbq[pId].contactType == ContactType::CT_NONPENETRATION || nbq[pId].contactType == ContactType::CT_BOUDNARY)
{
eta[pId] += min(nbq[pId].interpenetration, nbq[pId].interpenetration) / dt / dt / 15.0f;
}
}
接下来开始进行迭代求解 。迭代算法采用Jacobi迭代:
template <typename Coord, typename ContactPair>
__global__ void TakeOneJacobiIteration(
DArray<Real> lambda,
DArray<Coord> accel,
DArray<Real> d,
DArray<Coord> J,
DArray<Coord> B,
DArray<Real> eta,
DArray<Real> mass,
DArray<ContactPair> nbq,
DArray<Real> stepInv)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= J.size() / 4) return;
int idx1 = nbq[pId].bodyId1;
int idx2 = nbq[pId].bodyId2;
Real eta_i = eta[pId];
{
eta_i -= J[4 * pId].dot(accel[idx1 * 2]);
eta_i -= J[4 * pId + 1].dot(accel[idx1 * 2 + 1]);
if (idx2 != -1)
{
eta_i -= J[4 * pId + 2].dot(accel[idx2 * 2]);
eta_i -= J[4 * pId + 3].dot(accel[idx2 * 2 + 1]);
}
}
if (d[pId] > EPSILON)
{
Real delta_lambda = eta_i / d[pId];
Real stepInverse = stepInv[idx1];
if (idx2 != -1)
stepInverse += stepInv[idx2];
delta_lambda *= (1.0f / stepInverse);
//printf("delta_lambda = %.3lf\n", delta_lambda);
if (nbq[pId].contactType == ContactType::CT_NONPENETRATION || nbq[pId].contactType == ContactType::CT_BOUDNARY) // PROJECTION!!!!
{
Real lambda_new = lambda[pId] + delta_lambda;
if (lambda_new < 0) lambda_new = 0;
Real mass_i = mass[idx1];
if (idx2 != -1)
mass_i += mass[idx2];
if (lambda_new > 25 * (mass_i / 0.1)) lambda_new = 25 * (mass_i / 0.1);
delta_lambda = lambda_new - lambda[pId];
}
if (nbq[pId].contactType == ContactType::CT_FRICTION) // PROJECTION!!!!
{
Real lambda_new = lambda[pId] + delta_lambda;
Real mass_i = mass[idx1];
if (idx2 != -1)
mass_i += mass[idx2];
//if ((lambda_new) > 5 * (mass_i)) lambda_new = 5 * (mass_i);
//if ((lambda_new) < -5 * (mass_i)) lambda_new = -5 * (mass_i);
delta_lambda = lambda_new - lambda[pId];
}
lambda[pId] += delta_lambda;
//printf("inside iteration: %d %d %.5lf %.5lf\n", idx1, idx2, nbq[pId].s4, delta_lambda);
atomicAdd(&accel[idx1 * 2][0], B[4 * pId][0] * delta_lambda);
atomicAdd(&accel[idx1 * 2][1], B[4 * pId][1] * delta_lambda);
atomicAdd(&accel[idx1 * 2][2], B[4 * pId][2] * delta_lambda);
atomicAdd(&accel[idx1 * 2 + 1][0], B[4 * pId + 1][0] * delta_lambda);
atomicAdd(&accel[idx1 * 2 + 1][1], B[4 * pId + 1][1] * delta_lambda);
atomicAdd(&accel[idx1 * 2 + 1][2], B[4 * pId + 1][2] * delta_lambda);
if (idx2 != -1)
{
atomicAdd(&accel[idx2 * 2][0], B[4 * pId + 2][0] * delta_lambda);
atomicAdd(&accel[idx2 * 2][1], B[4 * pId + 2][1] * delta_lambda);
atomicAdd(&accel[idx2 * 2][2], B[4 * pId + 2][2] * delta_lambda);
atomicAdd(&accel[idx2 * 2 + 1][0], B[4 * pId + 3][0] * delta_lambda);
atomicAdd(&accel[idx2 * 2 + 1][1], B[4 * pId + 3][1] * delta_lambda);
atomicAdd(&accel[idx2 * 2 + 1][2], B[4 * pId + 3][2] * delta_lambda);
}
}
}
更新刚体的速度和位置信息。
template <typename Coord>
__global__ void RB_UpdateVelocity(
DArray<Coord> velocity,
DArray<Coord> angular_velocity,
DArray<Coord> accel,
Real dt)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= accel.size() / 2) return;
velocity[pId] += accel[2 * pId] * dt;
velocity[pId] += Coord(0, -9.8f, 0) * dt;
angular_velocity[pId] += accel[2 * pId + 1] * dt;
}
template <typename Coord, typename Matrix, typename Quat>
__global__ void RB_UpdateGesture(
DArray<Coord> pos,
DArray<Quat> rotQuat,
DArray<Matrix> rotMat,
DArray<Matrix> inertia,
DArray<Coord> velocity,
DArray<Coord> angular_velocity,
DArray<Matrix> inertia_init,
Real dt)
{
int pId = threadIdx.x + (blockIdx.x * blockDim.x);
if (pId >= pos.size()) return;
pos[pId] += velocity[pId] * dt;
rotQuat[pId] = rotQuat[pId].normalize();
rotMat[pId] = rotQuat[pId].toMatrix3x3();
rotQuat[pId] += dt * 0.5f *
Quat(angular_velocity[pId][0], angular_velocity[pId][1], angular_velocity[pId][2], 0.0)
*(rotQuat[pId]);
inertia[pId] = rotMat[pId] * inertia_init[pId] * rotMat[pId].inverse();
//inertia[pId] = rotMat[pId] * rotMat[pId].inverse();
}