宽阶段碰撞检测
刚体碰撞流程主要分为五部分。首先,对可能产生碰撞的n个刚体构建包围盒树(包括:AABB树(轴平行包围盒树,Aixe align bounding box tree)和OBB树(有向包围盒树),下述将以AABB树为例),将AABB树的根节点对应的区域,作为的碰撞区域;然后,使用Z空间填充曲线(Z-SFC)对碰撞区域进行划分,生成单元空间,并使用Morton码(莫顿码)对单元空间进行编码,生成Z空间填充曲线(Z-SFC)索引,以便后续构建内部节点的邻接关系;接着,根据生成的Z空间填充曲线(Z-SFC)索引自底向上、并行的构建压缩八叉树;其次,对构建出来的压缩八叉树进一步并行的恢复成完整的八叉树结构;最后,根据完整的八叉树自底向上的进行并行碰撞检测。接下来详细介绍每一个步骤:

1、构建AABB树
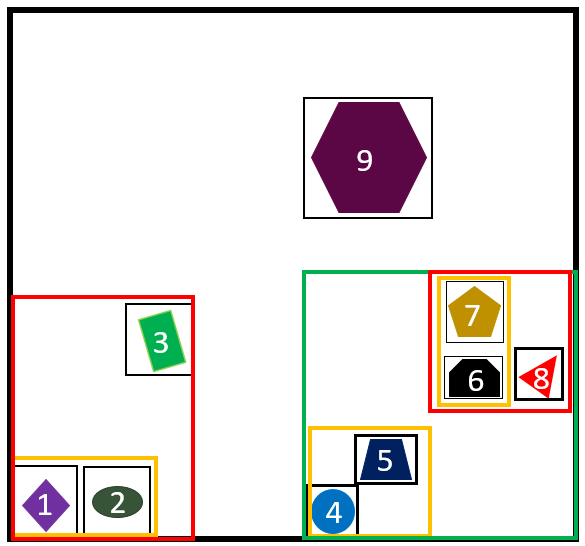
AABB树中每个子节点也是AABB树的结构,它只需要log(n)的时间复杂度就能完成节点的搜索过程。假设我们要检测刚体1-9的碰撞。根据刚体1-9的轮廓生成AABB包围盒。接下来通过执行以下操作来构建AABB树:
-
把刚体1作为AABB树的根节点;
-
把刚体2和刚体1作比较,判断刚体2与刚体1所在的区域有没有交集。如果有交集则继续判断刚体2是否与刚体1的子集有交集,将其加入到与节点1有公共交集的子集的最小的公共子节点之后。如果刚体2与刚体1没有交集,则根据刚体1和刚体2的区域重新生成一个公共区域,作为节点1和节点2的公共节点;
-
重复步骤b),直达把所有的节点都加入到AABB树中,并将AABB树的根节点对应的区域,作为的碰撞区域。
2、构建Z空间填充曲线(Z-SFC)和索引
Z空间填充曲线(Z-SFC)技术易于实现,并行化高,可用于将二维或三维空间中的区域进行有效的线性化。假设在D维空间中,将空间的每个维度均匀的分成k分,则会产生 个相等的非重叠的小空间单元。例如使用Z空间填充曲线(Z-SFC)对二维正方形区域进行划分,结果如下图所示;根据划分的结果按顺序进行标记:
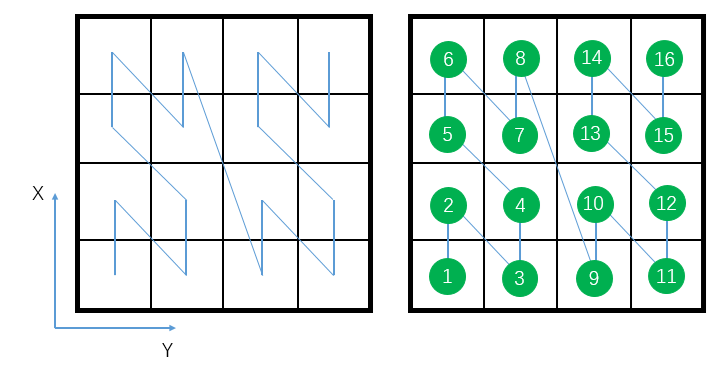
例如刚体1-9进行空间划分之后可得到:
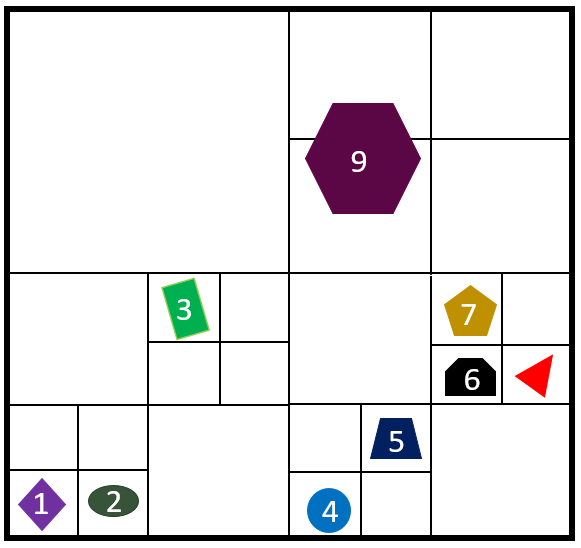
通常将划分的结果左下角的小单元空间设置为Z空间填充曲线(Z-SFC)的起点,并对区域进行Morton码编码。在二维空间中,假设存在刚体P的重心位置坐标为(x,y),则将该坐标作为叶子节点的坐标。经过Z空间填充曲线(Z-SFC)划分之后,该点所属的单元将为。对于刚体9横跨多个区域的需要进行去重操作$(\left\lfloor {{2^k}x/D} \right\rfloor ,\left\lfloor {{2^k}y/D} \right\rfloor )$,此时刚体9的Z空间填充曲线索引设置为数值最小的区域即11110000,并保存这几个区域的信息。二维空间创建Z空间填充曲线索引如下图所示:
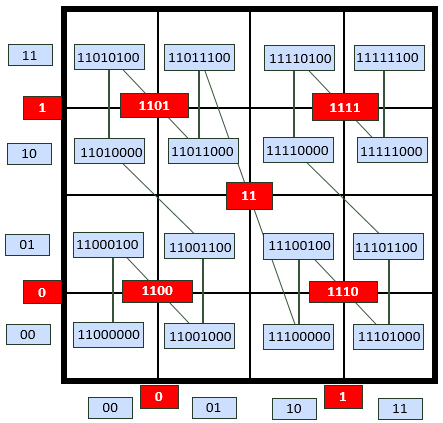
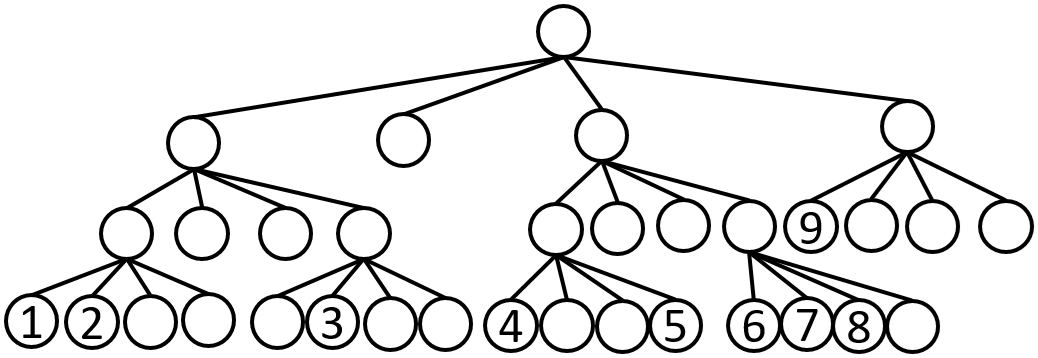
根据Z空间填充曲线(Z-SFC)索引,我们可以创建不同层级的Z空间填充曲线(Z-SFC),如下图所示:
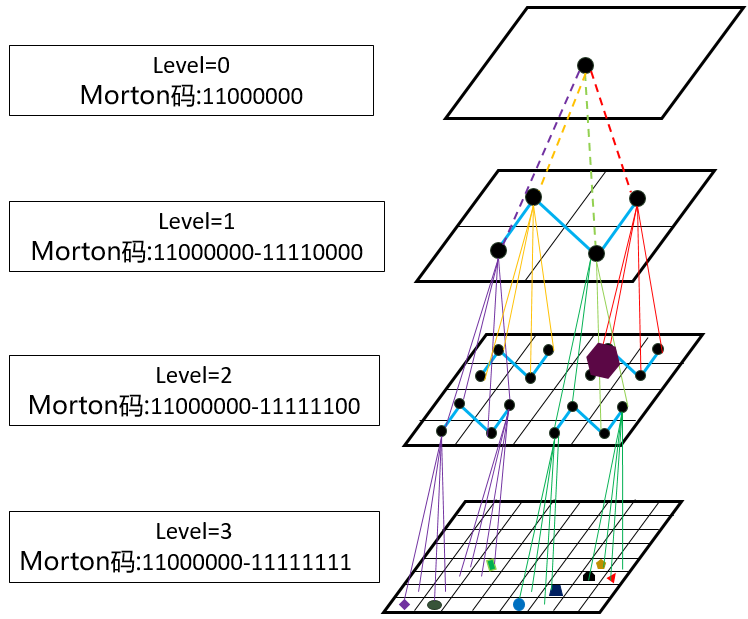
3、基于GPU的并行压缩八叉树的构建
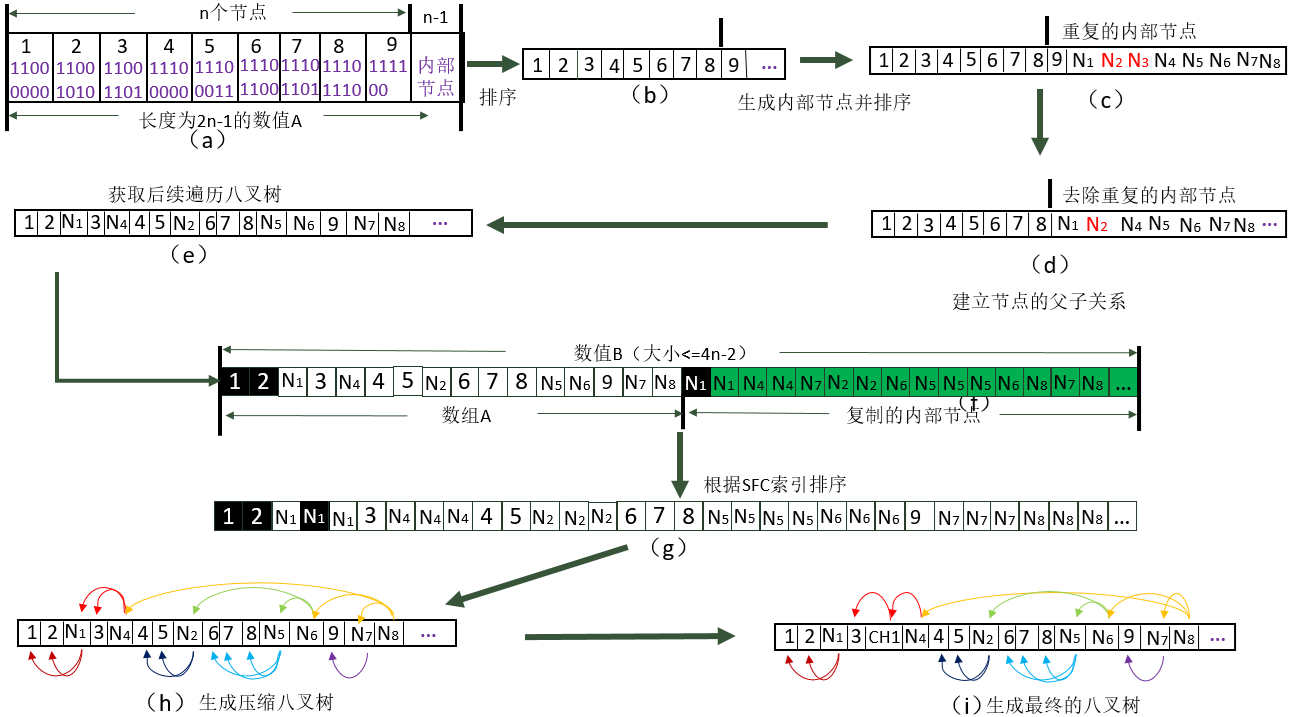
不同于CPU的八叉树构建,基于GPU的并行八叉树的构建是自底向上构建的。根据叶子节点所在的位置,反向生成内部节点,进而确定内部节点的关系,从而确定树的结构。自底向上生成树的过程适用于GPU并行计算。具体的实施过程如下图所示:
-
构建叶子节点
-
将待检测的刚体1-9作为输入点,使用长度为2n-1(n表示刚体的数量)的数组A保存这9个输入点作为叶子节点。
-
根据叶子节点的坐标生成Z空间填充曲线(Z-SFC)索引。
-
根据叶子节点的Z空间填充曲线(Z-SFC)索引,并行对数组A中的9个元素进行排序。
-
-
生成内部节点和八叉树的后序遍历 对每个相邻的叶子,使用Z空间填充曲线(Z-SFC)索引中的公共位并行的找出最小公共父节点(LCA)。例如,相邻叶子节点1和节点2的Z空间填充曲线(Z-SFC)索引分别为11000001和11000010,由此可得到节点1和节点2的最小公共父节点为11000000。
- 分配n − 1个GPU线程。
- 对于数组A中的每两个相邻叶子(例如数组A[i]和A[i + 1]),并行生成最小公共父节点,其最小公共节点的Z空间填充曲线索引为叶子节点A[i]和A[i + 1]的Z空间填充曲线索引的最大公共部分,并将其值存储在A[n + i]中。
- 根据公共节点的Z空间填充曲线索引,对不同层的内部节点进行并行排序。如果元素L1包含在元素L2中,则将L2元素置于L1元素之前;否则,将L1元素置于L2元素之前。图7中的(c)显示了排序后的内部节点,其中可能会生成重复项(N2和N3)。
- 在数组A的后半部分中,删除重复项。
- 对于没有相同Z空间填充曲线(Z-SFC)索引的两个相邻内部节点,并行地从当前节点开始遍历数组A的后半部分,删除它们重复的项。根据Z空间填充曲线(Z-SFC)索引对数组A进行并行排序,进而可以得到压缩八叉树的后序遍历。
-
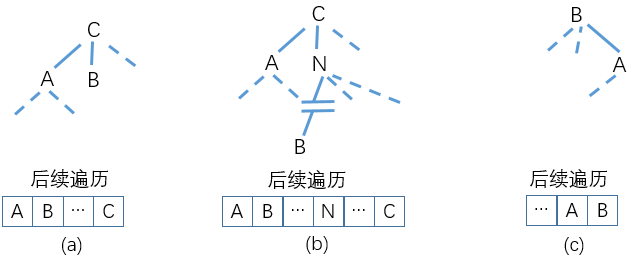
生成压缩八叉树 我们可以注意到数组A的末尾可能会有一些空元素。这是无法避免的,因为CUDA不支持动态内存分配和释放,因此必须在编译时就创建大小为2n−1的数组。然而仅仅得到八叉树的后续遍历还无法确定树的结构。(a)所示节点A和节点B属于同级的情况,因此它们的公共的父节点为C;(b)所示节点B是节点N的子节点,与节点A是相邻节点。(c)所示节点B是节点A的父节点。
为了进一步确定八叉树的内部结构,执行以下步骤:
- 分配两倍大小的叶子和内部节点数的数组B(最多4n-2)。将数组A复制到数组B中。
- 分配(叶子节点数+ 内部节点数-1)个GPU线程。
- 对于数组B的前半部分中的每两个相邻节点,根据Z空间填充曲线(Z-SFC)索引并行的生成最小公共父节点。例如对于数组B中的每两个相邻叶子B[i]和B[i + 1],并行生成内部节点,并将其存储在B[n + i]中。
- 根据Z空间填充曲线(Z-SFC)索引对生成的结果进行并行排序,将所有的内部节点和它们的副本将归并到一起。
- 对于具有相同Z空间填充曲线(Z-SFC)索引并且至少其中一个不是副本的节点,建立内部节点的父子关系。最终生成的压缩八叉树下图所示:
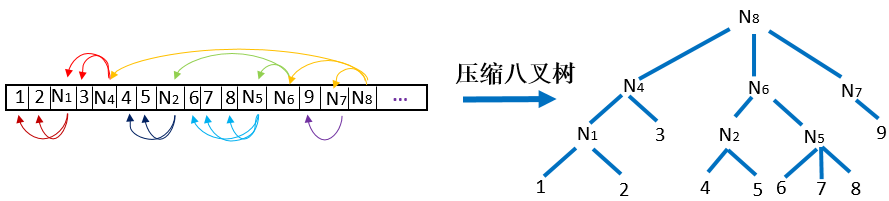
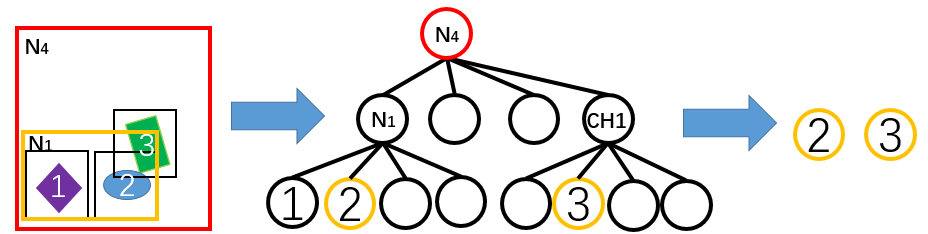
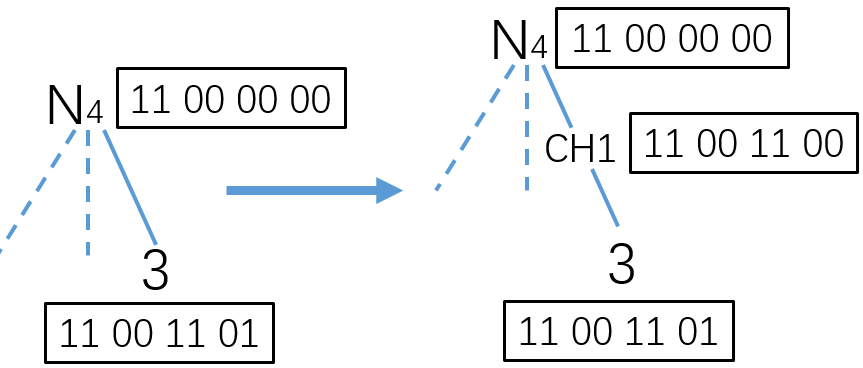
4、从压缩八叉树中恢复完整的八叉树
两个相邻的节点N4和节点3,其中节点3是节点N4的子节点。通过Z空间填充曲线(Z-SFC)索引来计算两个节点之间的深度差。例如节点N4和节点3的Z空间填充曲线(Z-SFC)索引分别为11000000和11001101,则深度差为2(节点N4处于深度1,节点3处于深度3,假设根深度为0)。这种差异表明压缩八叉树中缺少节点N4和节点3之间的中间节点。
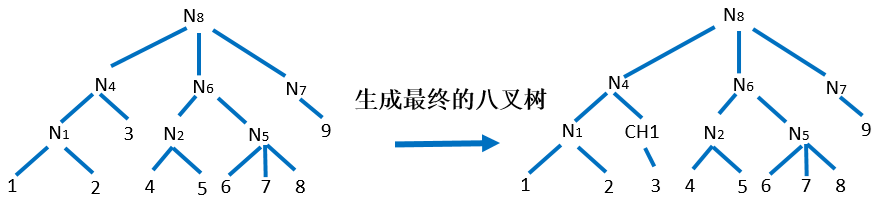
为了生成完整的八叉树结构执行:
- 分配大小等于数组A长度的线程,即(叶子数+内部节点数)。
- 计算每个节点与其父节点的深度差并累加,以获取插入内部节点所需的内存总数(由于GPU上不能进行动态的分配内存)。
- 根据每个节点与其父节点之间的深度差添加新的节点。当深度差大于1时,并行的在其中间插入新的节点。如下图所示,在节点N4和节点3之间插入了一个内部节点CH1,以获得完整八叉树结构。
5、使用八叉树结构自底向上的对刚体进行并行的碰撞检测
从叶子节点开始自底向上进行检测,当发现碰撞点时进一步进行细粒度检测,直到找到发生碰撞的叶子节点对。
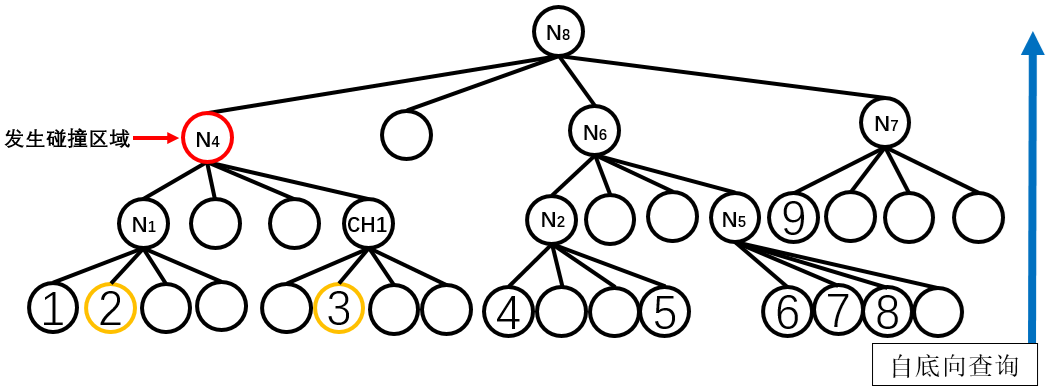
- 假设刚体2和刚体3发生了碰撞。针对待碰撞检测刚体,计算刚体所有八叉树层数及对应叶子节点,利用步骤4中八叉树自底向上查询所有重叠区域对应刚体的AABB包围盒。
- 如果找到碰撞包围盒,针对上述步骤中得到的AABB包围盒进一步对刚体2和刚体3的边界进行精确的碰撞检测,结果如下图所示: